English
What is noise?
Noise in an image is described as random granulation that is particularly visible in uniform areas.
Origins of noise
Noise in an image can stem from several different factors:
- Photonic noise: Classical light sources produce random variations in luminous flux which, after deflection in the optical system, produce the most common form of noise in photographic images.
- Thermal noise: Sensors can generate random signals due to the effect of ambient temperature.
- Transfer process noise: The process of charge transfer may be incomplete or interfere with adjacent photosites, thereby generating noise.
Definitions and units
Noise itself is characterized by several values, among which are Standard Deviation and Signal-to-Noise Ratio (SNR). Other measures are derived from these, such as Dynamic Range and Tonal Range. (Other aspects of interest include color sensitivity, and noise granulation and coloration, which will be discussed separately on this site.)
1. Standard Deviation
- Standard deviation of noise represents the dispersion of gray levels around the mean gray level, and is expressed in gray levels (GL).
,
where 
is the mean gray level measured in the patch.
2. Signal-to-Noise Ratio (SNR)
- SNR defines the purity of the output signal and gives direct information about the camera’s ability to reproduce a signal. On a logarithmic scale, it is expressed in decibels (dB), and is obtained from the following formula:
.
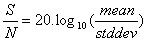SNR is independent of any gain applied to the signal since signal and noise are equally amplified.
3. Dynamic Range
Dynamic range is defined as the ratio between the highest and lowest gray luminance a sensor can capture. However, the lowest gray luminance makes sense only if it is not drowned by noise, thus this lower boundary is defined as the gray luminance for which the SNR is larger than 1. The dynamic range is a ratio of gray luminance; it has no defined unit per se, but it can be expressed in Ev, or f-stops.
4. Tonal Range
Tonal range is the effective number of gray levels the system can produce. This measure has to take noise into account (indeed, a very thin gray-level quantization is irrelevant if the quantization step is much smaller than noise). The standard deviation of noise can be viewed as the smallest difference between two distinguishable gray levels. The expression of the tonal range is
.
Since tonal range is a number with no unit, one can consider instead 
, which represents the number of bits necessary to encode all distinguishable gray levels.
DXOMARK encourages its readers to share comments on the articles. To read or post comments, Disqus cookies are required. Change your Cookies Preferences and read more about our Comment Policy.