Color depth

« Back to Glossary Index

Color sensors usually have three different types of photosites that are sensitive to light in different bands of wavelengths. Although there are other technologies, the overwhelming majority of color sensors use a Bayer color filter array. Each block of 4 contiguous photosites contains one photosite sensitive to low wavelengths (blue), one photosite sensitive to high wavelengths (red), and two identical photosites sensitive to medium wavelengths (green).

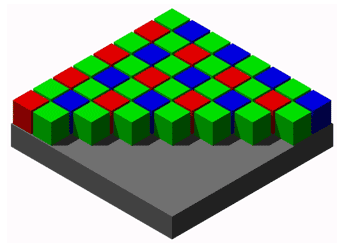
Since each channel has its own noise level, it actually distinguishes far fewer than the theoretical 10, 12, or 14 bits of RAW data. The sum of the tonal range on each channel gives a rough idea of the color sensitivity of a sensor, and experiments show that this sum is already fewer than 24 bits.

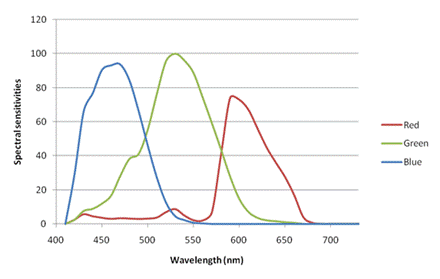
Moreover, the R, G, and B channels of a sensor are a consequence of its design. They are characterized by their spectral sensitivities, giving the proportion of incident photons that eventually reach the sensor for a given wavelength (called quantum efficiency). The figure below gives an example of spectral sensitivities of a sensor. Note that the photosites are frequently sensitive to near-infrared, so an infrared filter must be added to the system to filter out these wavelengths. In particular, note that these curves are not the color-matching functions .

Definitions

Color sensitivity is the number of reliably distinguishable colors up to noise. Roughly speaking, two colors are considered as distinguishable if their difference is larger than the noise. In this respect, color sensitivity is the generalization of color to the notion of tonal range.

To extend this idea for color data defining color sensitivity:

Let be the noise covariance matrix at the value (r, g, b).
For , let be the eigenvalues of this covariance matrix.

We call Color Sensitivity the number derived from

 .

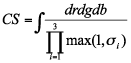The above formula shows that the determinant of the noise covariance matrix is the volume of the incertitude ellipsoid, in which the difference of two colors is most likely due to noise. However, because digital images are encoded using integer values, the dimensions of the incertitude ellipsoid are quantized. Hence the integrand in the equation above can be seen as the density of distinguishable colors around the point (r, g, b), and takes quantization into account. The integral itself can then be interpreted as the total number of colors that can be distinguished by the sensor.

As with tonal range, color sensitivity is a number with no unit, so instead we consider , which represents the number of bits necessary to encode all distinguishable color values.

SMI: Sensitivity Metamerism Index

The sensitivity metamerism index (SMI) is defined in the ISO standard 17321 and describes the ability of a camera to reproduce accurate colors. Digital processing permits changing color rendering at will, but whether the camera can or cannot exactly and accurately reproduce the scene colors is intrinsic to the sensor response and independent of the raw converter.

The underlying physics is that a sensor can distinguish exactly the same colors as the average human eye, if and only if the spectral responses of the sensor can be obtained by a linear combination of the eye cone responses. These conditions are called Luther-Ives conditions, and in practice, these never occur. There are objects that a sensor sees as having certain colors, while the eye sees the same objects differently, and the reverse is also true.

SMI is an index quantifying this property, and is represented by a number lower than 100 (negative values are possible). A value equal to 100 is perfect color accuracy, and is only attained when Luther-Ives conditions hold (which, as previously stated, never happens in practice). A value of 50 is the difference in color between a daylight illuminant and an illuminant generated by fluorescent tubes, which is considered a moderate error.

More precisely, SMI is defined as

 ,

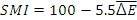where 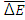 is the average CIELAB error observed on a set of various colors. In our experiments, we used the 18 colored patches of a Gretag McBeth color checker, as ISO 17321 recommends. The SMI varies depending on the illuminant.

In practice, the SMI for DSLRs ranges between 75 and 85, and is not very discriminating. It is different for low-end cameras (such as camera phones), which typically have a SMI of about 40. For this reason, we give this measurement as an indication but do not integrate it in DxO Mark.

Relative sensitivities and white balance scale

All the standard RGB color spaces (such as sRGB, Adobe RGB, Prophoto) assume that a neutral reflectance object (i.e., an object that reflects every wavelength equally) has equal values on the three channels. However, the RAW values on the sensor depend on the spectrum of the light illuminating the neutral object, and on the spectral responses of the sensor. The three channels are usually different. The relative sensitivity of both the red and blue channels is the ratio between the value of the red (or blue) channel and the green channel.

The SMI depends both on the illuminant and the spectral responses of the sensor. Typically, with a tungsten illuminant, the blue sensitivity is very low, due to the weak sensitivity of silicon in short wavelengths and the lack of short wavelengths in tungsten light.

For design reasons, relative sensitivities are almost always lower than 1.

White balance scales are the digital gains applied on each channel to compensate for the lack of sensitivity in the red and blue channels. After applying the white balance, red, green and blue should be equal on a neutral object.

White balance scales are simply the inverse of the relative sensitivity. However, we think the redundancy is interesting and expresses two different factors: On the one hand, relative sensitivity is an objective characteristic of the sensor; on the other hand, white balance scale is what image science engineers apply to compensate for the differences in sensitivity.

Large white balance scales have a major influence on image quality since they directly impact noise, and this is taken into account in the color sensitivity measurement.

Channel decomposition and color matrix

Assume that the three channels of a sensor have equal sensitivities (or, equivalently, that white balance has been applied). In practice, the primaries of the sRGB color space do not correspond with the primaries of the sensor. (See the explanation for Luther-Ives condition in the section SMI above.) For each sensor channel, the channel decomposition describes the linear combination of the primaries of the sRGB color space that best fits the sensor channel. Typically, the red sensor channel is expected to contain mostly red, a bit of green, and almost no blue. A decomposition of the red channel close to (1,0,0) shows that the red channel of the sensor is very “pure.”

The color matrix gives the coefficients of the linear combination of the sensor channels which have to be applied to compensate for the sensor channels’ lack of purity as compared to the sRGB primaries. As with the white balance scales and the relative sensitivities, the channel decomposition and the color matrix give exactly the same information in a complementary manner. The channel decomposition coefficient can be portrayed as a 3×3 matrix, which means that the color matrix is then simply the inverse of the channel decomposition coefficient matrix.

The channel decomposition is a low-level description of the sensor spectral response, while the color matrix is what engineers use to make the sensor react as though it had sRGB primaries.

A color matrix with large singular values yields a dramatic amplification of noise, and this is taken into account in the color sensitivity measurement.

Full-color sensitivity

The noise on the sensor is processed by a RAW converter to lead to the final image. In particular, RAW converters apply a color rendering which maps the RAW values to RGB values in the final image (for instance, sRGB values). Color rendering includes at least white balancing and a color matrix, as described above. These steps yield an amplification of noise. For each triple RGB in the final image, noise can be predicted from the RAW noise characteristics, the white balance scales, and the color matrix coefficients. The noise on the three color channels is described by a three-dimensional covariance matrix, which is not easy to represent. In the full-color sensitivity tab, we chose to illustrate the noise in the (a,b) plane of the CIE Lab color space. For different values of luminance and different ISO sensitivities, the noise at given colors is represented by an ellipse which shows the colors that are likely to be generated in the image instead of the real color (displayed at the ellipse center). The orientation and the size of the ellipses show the coloration of noise and its amplitude.

« Back to Glossary Index